Section 3.1 – Basic Terminology¶

definition: A function from a set $A$ to $B$ is a binary relation where every element in $A$ corresponds to exactly one element in $B$. We write,

$$f: A \to B$$

"$f$ is a function from $A$ to $B$".

We typically define functions using equations (e.g. $f(x) = x^2$) but they can also be lists.

Example

$$\begin{aligned} A &= \{ 1,2,3,4 \} \newline B &= \{ w,x,y,z \} \newline \end{aligned}$$

Sub-example¶

$$\begin{aligned} f &= \{ (1,x), (2,y), (3,w), (4,y) \} \end{aligned}$$

This is a function since everything in $A$ corresponds to one thing in $B$. It's okay for multiple things in $A$ to go to one thing in $B$.

Sub-example¶

$$\begin{aligned} g = \{ (1,x), (2,y), (3,z) \} \end{aligned}$$

This is not a function since $4$ is not mapped to anything.

Sub-example¶

$$\begin{aligned} h = \{ (1,x),(2,x),(3,x),(4,x) \} \end{aligned}$$

This is a function.

Sub-example¶

$$\begin{aligned} i = \{ (1,y),(2,z),(2,x),(3,w),(4,x) \} \end{aligned}$$

This is not a function since $2$ corresponds to two values.

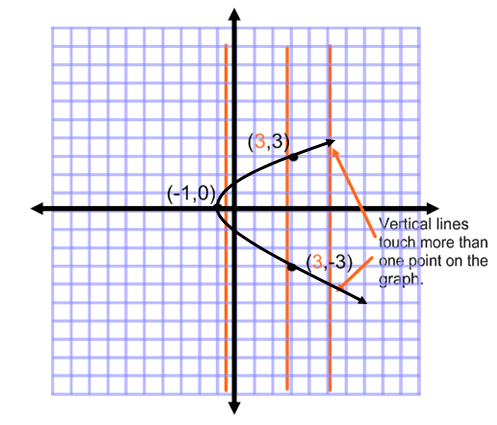
Recall¶

The vertical line test.

This is a function since every point in $x$ maps to one point in $y$.

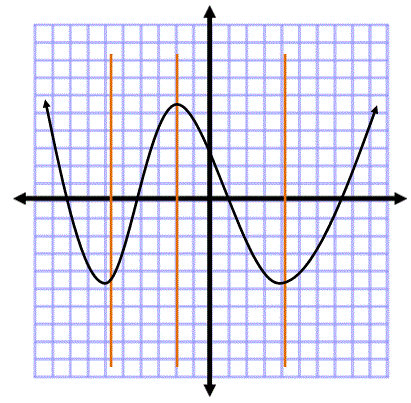
This is not a function since some points in $x$ correspond to two values of $y$.

Notation¶

if $(a,b) \in f$ then we write,

$$\begin{aligned} &f(a) = b \newline &f : a \mapsto b \newline \end{aligned}$$

where $b$ is the image of $a$.

Onto and One-to-One¶

definitions: For a function $f: A \mapsto B$,

• $f$ is onto (or subjective) if $\forall b \in B, \exists a \in A$ such that $f(a) = b$.
• $f$ is one-to-one (or injective) if all elements of $A$ map to different elements of $B$.
  • intuitive definition: if $x_1 \neq n_2 \Rightarrow f(x_1) \neq f(x_2)$
  • proof definition: if $f(x_1) = f(x_2) \Rightarrow x_1 = x_2$

Example

$$\begin{aligned} F &: A \mapsto B\newline A &= \{ 1,2,3,4 \} \newline B &= \{ w,x,y,z \} \newline \end{aligned}$$

$$\begin{aligned} f &= \{ (1,y), (2,w), (3,x), (4,z) \} \end{aligned}$$

Solution

This is onto since every element in $B$ is mapped to. It is also one-to-one since every element in $A$ points to something different.

Domain¶

For a function $f: A \mapsto B$,

• the domain of $f$ is $A$
• the target of $f$ is $B$
• the range of $f$ the set ${ b \in B, \exists a \in A, f(a) = b }$

Functions with Formulas¶

Example

$$f(x) = \frac{3x + 4}{5}$$

where $f: \mathbb Z \mapsto \mathbb R$.

Is $f$ one-to-one or onto?

Solution

Required to Prove One-to-One¶

Suppose $f(x_1) = f(x_2)$ then $x_1 = x_2$.

So¶

Suppose $f(x_1) = f(x_2)$,

$$\begin{aligned} \frac{3x_1 + 4}{5} &= \frac{3x_2 + 4}{5} \newline 3x_1 + 4 &= 3x_2 + 4 \newline 3x_1 &= 3x_2 \newline x_1 &= x_2 \newline \end{aligned}$$

$$\therefore \text{One-to-one}$$

Required to Prove Onto¶

We need $b \in \mathbb R$ such that $a \in \mathbb Z$ where $f(a) = b$.

So¶

Suppose $b \in \mathbb R$ such that $a \in \mathbb Z$ where $f(a) = b$.

$$\begin{aligned} b &= \frac{3a + 4}{5} \newline 5b &= 3a + 4 \newline 5b - 4 &= 3a \newline \frac{5b - 4}{3} &= a \in \mathbb Z \newline \end{aligned}$$

Consider $b = 1$,

$$\begin{aligned} \frac{5\cdot1 - 4}{3} &= \frac{1}{3} \notin \mathbb Z \newline \end{aligned}$$

$$\therefore \text{Not onto}$$

Solution

If $f: \mathbb R \mapsto \mathbb R$ instead.

Supposed $b \in \mathbb R$ and suppose $\exists a in \mathbb R$ such that $f(a) = b$.

Then,

$$\begin{aligned} a &= \frac{5b - 4}{3} \newline &\in \mathbb R \newline \end{aligned}$$

$$\therefore \text{Onto}$$

Example

Let $f: \mathbb R \mapsto \mathbb R$ where,

$$\begin{aligned} f(x) = x^2 + 1 \newline \end{aligned}$$

Solution

Not one-to-one since,

$$\begin{aligned} (-1)^2 + 1 &= (1)^2 + 1 \newline \text{but } -1 &\neq 1 \newline \end{aligned}$$

Not onto since,

$$\begin{aligned} x^2 + 1 &\ge 1 \newline \text{and } 0 &\in \mathbb R \newline \therefore \not\exists a \in \mathbb R, f(a) &= 0 \end{aligned}$$

Bijection¶

definition: If a function $f$ is both one-to-one and onto it is a bijection.

Functional Equality¶

definition: Two functions, $f$ and $g$ are equal if,

1. They have the same target
2. They have the same domain
3. $f(x) = g(x)$, $\forall x \in$ domain

Floor and Ceiling¶

definition: The floor of $x$ is the function,

$$\begin{aligned} f(x) = \lfloor x \rfloor, f: \mathbb R \mapsto \mathbb Z \end{aligned}$$

Example

definition: The ceiling of $x$ is the function,

$$\begin{aligned} f(x) = \lceil x \rceil, f: \mathbb R \mapsto \mathbb Z \end{aligned}$$

Function Equality¶

definition: Two functions $f$ and $g$ are equal if:

• They have the same target
• They have the same domain
• $f(x) = g(x)$ for all $x$ in the domain of $f$

Example

Let $f: \mathbb R \mapsto \mathbb Z$ defined by,

$$f(x) = \lfloor x \rfloor$$

and let $g: \mathbb Z \mapsto \mathbb Z$ defined by,

$$g(x) = \lfloor x \rfloor$$

and let $h: \mathbb Z \mapsto \mathbb R$ defined by,

$$h(x) = \lfloor x \rfloor$$

Solution

$f \neq g$ since they have different domains but the range of $h$ is equal to the range of $g$. However since they have different targets $h \neq g$.

Special Functions¶

definition: For any set $A$ the identity function, $i_A: A \mapsto A$, where,

$$i_A (x) = x, \forall x \in A$$

we can also say this is the set of ordered pairs, $i_A = { (a,a): a \in A }

definition: The absolute value of $x$, $|x|$ is defined as,

$$\left|x\right| = \left\{ \begin{array}{lr} x & \text{ if } x \ge 0 \newline -x & \text{ if } x \lt 0 \newline \end{array} \right.$$