Lecture 16 - Notes

March 7, 2016

Planar Graphs Continued

Euler Relation

definition: The Euler Relation is, given a planar graph,

$$\begin{aligned} f + v = e + 2 \end{aligned}$$

where $f$ is the number of faces, $v$ is the number of vertices and $e$ is the number of edges.

Proof

Imagine we're invading Rome and we want to first flood all the fields around Rome then destroy all roads leading to Rome. How many edges do we destroy?

To flood the regions we need to break a dyke leading into every region, so $f-1$ dykes (edges in this case).

To destroy the roads we have to destroy $v - 1$ roads.

So,

$$\begin{gathered} (f-1) + (v-1) = e \\\\ \downarrow \\\\ f + v = e + 2 \\\\ \end{gathered}$$

Geometric Dual

definition: We define the Geometric Dual of a planar graph $G$ as the graph created if we make a vertex out of every face of $G$.

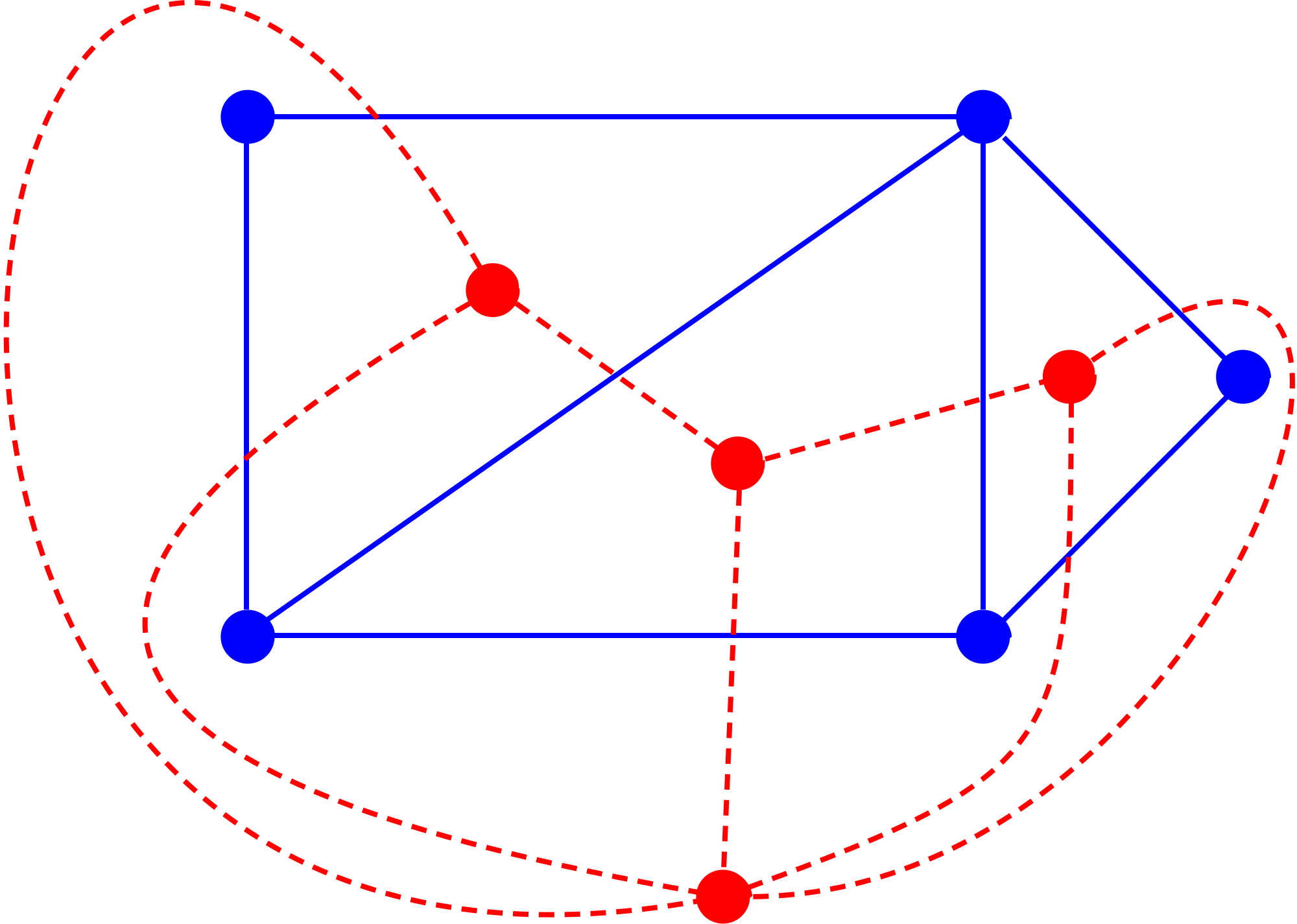
If all faces are incident on at least $3$ edges then,

$$\begin{gathered} 3f \le 2e \\\\ \downarrow \\\\ 3e + 6 = 3v + 3f \le 3v + 3e \\\\ e \le 3v - 6 \end{gathered}$$

Theorem

If a Planar Graph without self-loops or multi-edges,

$$\begin{aligned} e \le 3v - 6 \end{aligned}$$

Genus

definition: The Genus of a graph is defined as the degree of the surface required to embed the graph on the surface. It is related to the graph by,

$$\begin{aligned} \text{genus} &= \frac{1}{2} \left( 2 - v + e - f \right) \end{aligned}$$

Here's some examples of different genus,

Genus 0	Genus 1	Genus 2	Genus 3

Embedding in a Plane

Pre-Processing

1. Break a Graph into its connected components
2. Break each component down to 2-connected components (subgraphs with no cut vertices)