Lecture 9 - Notes

February 1, 2016

Probability

How many people does it take before the probability that two have the same birthday is more than 50%?

Let's assume that all birthdays are equally likely, what's the probability that $n$ people have different birthdays?

So,

$$\begin{align} p &= \frac{\text{favourable cases}}{\text{total number of cases}} \\\\ &= \frac{\binom{365}{n}n!}{365^n} \end{align}$$

we could also think of this as,

$$\begin{align} \frac{365}{365} \cdot \frac{364}{365} \cdot \frac{363}{365} \cdot \ldots \cdot\frac{365-n}{365} \end{align}$$

let's rewrite this where $D$ is the days,

$$\begin{align} \left( 1 - \frac{0}{D}\right)\left( 1 - \frac{1}{D}\right)\left( 1 - \frac{2}{D}\right)\ldots\left( 1 - \frac{n-1}{D}\right) = S_n \end{align}$$

we're asking when,

$$\begin{align} 1 - S_n \ge \frac{1}{2} \end{align}$$

Now, when $x$ is small $1 - x \approx e^x$, so if $n$ is small compared with $D$ then,

$$\begin{align} \prod_{j=1}^{n-1} (1 - \frac{j}{D}) &\approx \prod_{j=1}^{n-1} e^{-\frac{j}{D}}\\\\ &= e^{\left( -\sum_{j=1}^{n-1} \frac{j}{D} \right)} \\\\ &= e^{\left(\frac{-n\left( n-1 \right)}{2D} \right)} \\\\ &\approx e^{\left(\frac{- n^2}{2D} \right)} \\\\ \end{align}$$

so the probability is $\frac{1}{2}$ when,

$$\begin{align} \frac{n^2}{2D} &= \ln \frac{1}{2} \\\\ \frac{n^2}{2D} &= \ln 2 \\\\ n &= \sqrt{2 \ln 2} \cdot \sqrt{D} \\\\ &= \sqrt{\ln 4} \cdot \sqrt{D} \\\\ &\approx 1.1774 \cdot \sqrt{D} \\\\ \end{align}$$

Harmonic Numbers

definition: The harmonic numbers are a series denoted,

$$\begin{align} H_n = 1 + \frac{1}{2} + \frac{1}{3} + \ldots + \frac{1}{n} \end{align}$$

The harmonic numbers arise in analyzing many algorithms.

Example

Consider $f(x) = \frac{1}{x}$,

Mean Time to Failure

When do you get the first heads when flipping coins?

We can draw the outcomes,

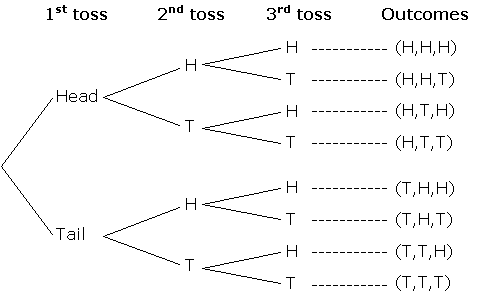
Let $p$ be the probability of a failure (a heads) and $p_k$ be the probability of a failure on the $k$-th try. We can write $p_k$ as

$$\begin{align} p_k = \left( 1 - p \right)^{k-1}p \end{align}$$

which we can see,

$$\begin{align} \sum_{k \ge 1} p_k &= \sum_{k \ge 1} \left( 1 - p \right)^{k-1}p \\\\ &= p \sum_{k \ge 0} \left( 1 - p \right)^{k} \\\\ &= p \frac{1}{1-(1-p)} \\\\ &= \frac{p}{p} \\\\ &= 1 \\\\ \end{align}$$

so all our probabilities sum to one (which is good).

Uniform Hashing

You're a coupon collector and you're trying to collect $n$ coupons. How many do I need to collect before I can expect to have them all?

Let $X$ be the number of trials.